Surveying I– coordinate account

Page takes part in the competition "Notes on the Internet" organized by the Rector of Academy of Science and Technology in Cracow.
V o t e !

Back>>

Calculation of coordinates of points on offset

Method offset (ordinate and abscissa) is primarily used to calculated coordinates of the points of measurement situations.

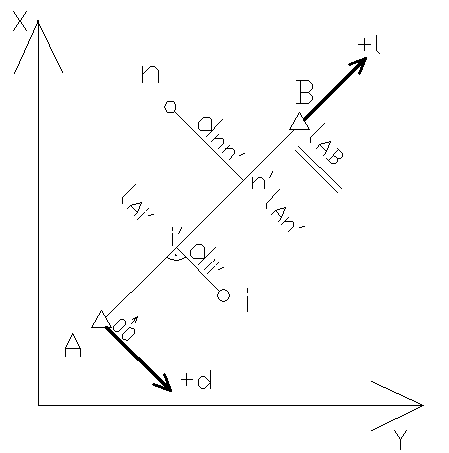
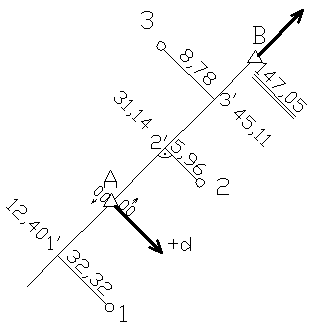
Figure 1. Sketch of measurement points by the ordinate and abscissa in the local coordinate system (axis + l corresponds to the line AB and the axis + h is perpendicular to it, and addressed to the right)

Search:
i (X_i, Y_i)
n (X_n, Y_n)


Data:
A (X_A, Y_A)
B (X_B, Y_B)

Measured:
d_ii'
d_nn'
l_Ai'
l_An'
l_AB


The task of calculating coordinates of points on offset should start from the coordinates designate the distance between the known points A and B, the following formula: L_AB = √________ Δx² + Δy², where Δx = X_B – X_A, Δy = Y_B – Y_A. Then, between the measured length l_AB, and calculated from the coordinates L_AB we calculated deviation f, which must meet the criteria specified in the User's G-4 such that f ≤ f_l, where f = Ιl_AB – L_ABΙ. If your deviation is within the limit, we can proceed further accounts.

In calculating the coordinates of the point and, which is located on the right side, use the following formula:

X_i = X_A + Δx_Ai' – Δx_ii'
Y_i = Y_A + Δy_Ai' + Δy_ii',

where:

Δx_Ai' = l_Ai'Δx l_AB


Δy_Ai' = l_Ai' Δy l_AB


Δx_ii' = d_ii'Δy l_AB


Δy_ii' = d_ii' Δx l_AB

In calculating the coordinates of point n on the left side, using the following formula:

X_n = X_A + Δx_An' + Δx_nn'
Y_n = Y_A + Δy_An' – Δy_nn',

where:

Δx_An' = l_An'Δx l_AB


Δy_An' = l_An' Δy l_AB


Δx_nn' = d_nn'Δy l_AB


Δy_nn' = d_nn' Δx l_AB

Control calculation:
1) verify that the sum of the differences severed Δl is equal to the length measured l_AB:

∑Δl = l_AB

2) verify that the sum of elevation difference Δd is equal to 0:

∑Δd = 0

3) calculation of the coordinates of point of B with the calculated coordinates of points on offset:

X_B = X_i + Δx_Bi' + Δx_ii'
Y_B = Y_i + Δy_Bi' – Δy_ii',

where:

Δx_Bi' = (l_AB – l_Ai')Δx l_AB


Δy_Bi' = (l_AB – l_Ai') Δy l_AB


Δx_ii' = d_ii'Δy l_AB


Δy_ii' = d_ii' Δx l_AB




X_B = X_n + Δx_Bn' – Δx_nn'
Y_B = Y_n + Δy_Bn' + Δy_nn',

where:

Δx_Bn' = (l_AB – l_An')Δx l_AB


Δy_Bn' = (l_AB – l_An') Δy l_AB


Δx_nn' = d_nn'Δy l_AB


Δy_nn' = d_nn' Δx l_AB

The following table is presented, which facilitates the performance of the control method 1) and 2).

Example

Calculate the coordinates of points 1, 2 and 3 on offset.

Data:
A (212,31m; 588,23m)
B (291,32m; 712,21m)

Measured:
d_11' = 32,32m
d_22' = 5,96m
d_33' = 8,78m
d_AB = 147,05m
d_A1' = -12,40m
d_A2' = 31,14m
d_A3' = 45,11m

SOLUTION

Δx_AB = X_B – X_A = 79,01m
Δy_AB = Y_B – Y_A = 123,98m


L_AB = √____________ Δx_AB² + Δy_AB²


L_AB = √________________ 79,01² + 123,989²


D_AB = 147,02m


f = Ιl_AB – L_ABΙ = Ι147,05 – 147,02Ι = 0,03m
f_l = 0,07m

The condition f ≤ f_l is satisfied.



Calculation of coordinates of a point number1

X₁ = X_A + Δx_A1' – Δx_11' = 212,31 + (-6,66) – 27,25 = 178,40m
Y₁ = Y_A + Δy_A1' + Δy_11', = 588,23 + (-10,45) + 17,37 = 595,15m

where:

Δx_A1' = l_A1'Δx l_AB


Δx_A1' = -12,40 79,01 147,05


Δx_A1' = -6,66m


Δy_A1' = l_A1' Δy l_AB


Δy_A1' = -12,40 123,98 147,05


Δy_A1' = -10,45m


Δx_11' = d_11'Δy l_AB


Δx_11' = 32,32 123,98 147,05


Δx_11' = 27,25m


Δy_11' = d_11' Δx l_AB


Δy_11' = 32,32 79,01 147,05


Δy_11' = 17,37m




Calculation of coordinates of a point number 2

X₂ = X_A + Δx_A2' – Δx_22' = 212,31 + 16,73 – 5,02 = 224,02m
Y₂ = Y_A + Δy_A2' + Δy_22', = 588,23 + 26,25 + 3,20 = 617,68m

where:

Δx_A2' = l_A2'Δx l_AB


Δx_A2' = 31,14 79,01 147,05


Δx_A2' = 16,73m


Δy_A2' = l_A2' Δy l_AB


Δy_A2' = 31,14 123,98 147,05


Δy_A2' = 26,25m


Δx_22' = d_22'Δy l_AB


Δx_22' = 5,96 123,98 147,05


Δx_22' = 5,02m


Δy_22' = d_22' Δx l_AB


Δy_22' = 5,96 79,01 147,05


Δy_22' = 3,20m




Calculation of coordinates of a point number 3

X₃ = X_A + Δx_A3' + Δx_33' = 212,31 + 24,24 + 7,40 = 243,95m
Y₃ = Y_A + Δy_A3' – Δy_33', = 588,23 + 38,03 – 4,72 = 617,68m

where:

Δx_A3' = l_A3'Δx l_AB


Δx_A3' = 45,11 79,01 147,05


Δx_A3' = 24,24m


Δy_A3' = l_A3' Δy l_AB


Δy_A3' = 45,11 123,98 147,05


Δy_A3' = 38,03m


Δx_33' = d_33'Δy l_AB


Δx_33' = 8,78 123,98 147,05


Δx_33' = 7,40m


Δy_33' = d_33' Δx l_AB


Δy_33' = 8,78 79,01 147,05


Δy_33' = 4,72m

Control

Point number	Abscissa l	Ordinate d	Differences Δl	Differences Δd
A	0,00	0,00	-12,40	32,32
1	-12,40	32,32	43,54	-26,36
2	31,14	5,96	13,97	-14,74
3	45,11	-8,78	101,94	8,78
B	147,05	0,00	147,05	0,00

Calculation of coordinates of a point B from point 1 coordinates

X_B = X₁ + Δx_B1' + Δx_11' = 178,40 + 85,67 + 27,25 = 291,32m
Y_B = Y₁ + Δy_B1' – Δy_11', = 595,15 + 134,43 – 17,37 = 712,21m

where:

Δx_B1' = (l_AB – l_A1')Δx l_AB


Δx_B1' = 159,45 79,01 147,05


Δx_B1' = 85,67m


Δy_B1' = (l_AB – l_A1') Δy l_AB


Δy_B1' = 159,45 123,98 147,05


Δy_B1' = 134,43m


Δx_11' = d_11'Δy l_AB


Δx_11' = 32,32 123,98 147,05


Δx_11' = 27,25m


Δy_11' = d_11' Δx l_AB


Δy_11' = 32,32 79,01 147,05


Δy_11' = 17,37m




Calculation of coordinates of a point B from point 2 coordinates

X_B = X₂ + Δx_B2' + Δx_22' = 224,02 + 62,28 + 5,02 = 291,32m
Y_B = Y₂ + Δy_B2' – Δy_22', = 617,68 + 97,73 – 3,20 = 712,21m

where:

Δx_B2' = (l_AB – l_A2')Δx l_AB


Δx_B2' = 115,91 79,01 147,05


Δx_B2' = 62,28m


Δy_B2' = (l_AB – l_A2') Δy l_AB


Δy_B2' = 115,91 123,98 147,05


Δy_B2' = 97,73m


Δx_22' = d_22'Δy l_AB


Δx_22' = 5,96 123,98 147,05


Δx_22' = 5,02m


Δy_22' = d_22' Δx l_AB


Δy_22' = 5,96 79,01 147,05


Δy_22' = 3,20m




Calculation of coordinates of a point B from point 3 coordinates

X_B = X₃ + Δx_B3' – Δx_33' = 243,95 + 54,77 – 7,40 = 291,32m
Y_B = Y₃ + Δy_B3' + Δy_33', = 621,54 + 85,95 + 4,72 = 712,21m

where:

Δx_B3' = (l_AB – l_A3')Δx l_AB


Δx_B3' = 101,94 79,01 147,05


Δx_B3' = 54,77m


Δy_B3' = (l_AB – l_A3') Δy l_AB


Δy_B3' = 101,94 123,98 147,05


Δy_B3' = 85,95m


Δx_33' = d_33'Δy l_AB


Δx_33' = 8,78 123,98 147,05


Δx_33' = 7,40m


Δy_33' = d_33' Δx l_AB


Δy_33' = 8,78 79,01 147,05


Δy_33' = 4,72m